
|
What is an Euler-Fokker genus?
In ancient times the Greeks made a distinction between different genera.
The fourth was the interval between the two extreme tones of the tetrachord.
Two other tones divided this distance into three intervals, in various
different ways. This multiformity gave rise to a system of classification into
genera: the enharmonic, the chromatic and the diatonic genus.
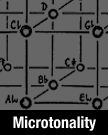
Bb- 3 F- 3 C- 3 G-
7 7 7 7
C 3 G 3 D 3 A
7 7 7 7
D+ 3 A+ 3 E+ 3 B+
[55777] {C,C#} can be sketched as follows:
F 5 A 5 C#
7 7 7
G+ 5 B+ 5 D#+
7 7 7
Bb- 5 D- 5 F+
7 7 7
C 5 E 5 G#
In this network the horizontal connections represent major thirds, and the vertical ones harmonic sevenths. After stacking the intervals, the tones are transposed down as many octaves as necessary to bring them inside the range of one octave. One can choose the name of the fundamental at will, like D+ in the first example. These genera have been employed by Alan Ridout. We can clarify this first example by giving the frequency ratios:
0: 1/1 C 0.000 cents
1: 9/8 D 203.910 cents
2: 8/7 D+ 231.174 cents
3: 9/7 E+ 435.084 cents
4: 21/16 F- 470.781 cents
5: 189/128 G- 674.691 cents
6: 3/2 G 701.955 cents
7: 27/16 A 905.865 cents
8: 12/7 A+ 933.129 cents
9: 7/4 Bb- 968.826 cents
10: 27/14 B+ 1137.039 cents
11: 63/32 C- 1172.736 cents
12: 2/1 C 1200.000 cents
The number of intervals which form the basis of an Euler-Fokker genus is called the degree. The genera [33377] and [55777] are genera of the fifth degree. Genera of a particular degree do not all have to have the same number of tones. The number of tones also depends on the exponents of the basic intervals. ([33355] can also be notated as [3³.5²].) The degree is thus the sum of the exponents. One obtains the number of tones by increasing all exponents with one and taking the product of that. So [3³.5²] has (3+1)×(2+1) = 12 tones. It's written sometimes also as [2m.3³.5²] to indicate the arbitrariness of the number of octaves, as in the following figure:
Each line herein depicts one tone of the frequency spectrum. The regular and
sometimes irregular character of the genera becomes visible this way.
They are of the third degree, so with three, not necessarily different,
generating factors. The tone lattice of the first three is 1-dimensional
(they contain one factor), the next ones 2-dimensional and only the last one is
3-dimensional because of the three different generating intervals
3, 5 and 7 - ignoring the octave with factor 2.
An Euler-Fokker genus can also be defined as a complete contracted chord.
This term is Fokker's. The term complete chord comes from Euler. A complete
chord has a fundamental and a guide tone, with in between all tones that are both a
whole multiple of the fundamental, and a divisor of the guide tone. The guide tone is
also a whole multiple of the fundamental. For example if we take the number 1 for the
fundamental, and the number 12 for the guide tone, then the complete chord consists
of the tones 1, 2, 3, 4, 6 and 12. We can also reverse this and say that no tones can
be added to a complete chord without altering the ratio of the fundamental to the guide tone.
This quotient of guide tone and fundamental is called the tension number
or exponens (by Euler: Exponens consonantiae).
The genera of the third degree are preprogrammed among others on the
12-tone manual of the Fokker-organ.
Although the Euler-Fokker genera are strictly speaking tuned pure (just), they
can also be played in the 31-tone equal tempered system because the three
basic intervals are well approximated in it.
The beatings caused by the slight impurity make the sound of them more lively.
The major third in 31-tone equal temperament is formed by 10 steps, the fifth
by 18 steps and the harmonic seventh by 25 steps.
Manuel Op de Coul, 2000
Literature
SoftwareWith the computer program Scala it's possible to calculate Euler-Fokker genera with arbitrary factors and of any degree and analyse them.
|









 and
and  signs respectively. Bb- (3
steps lower than B) is B
signs respectively. Bb- (3
steps lower than B) is B en C#+ is
C
en C#+ is
C .
. ,B}
,B} }
}