Equal Temperament and the Thirty-one-keyed organ
There are a great many musics among the people inhabiting our planet, and they
show differences as great as the languages spoken by the various races and
nations. In addition, there is the music of the birds, and there are melodic
lines of human speech. It is a very difficult task to represent all this music
by written symbols. This task requires centuries of analyzing and systematizing
work. Too soon one is eager to believe that one's own music is the most
natural, and that one's own way of putting it on paper in notes on staves is
the most straightforward and efficient way of recording it, and that there is
no alternative. The fact is, however, that our subdivision of the interval of
the octave into 12 equal semitones represents a solution for certain special
needs only. It embodies a stage in the historical development of the art, a
system with its virtues and its deficiencies, and one that is likely to be
modified or even relinquished during the course of historical evolution. There
are vast civilizations of autochtonic musics, not very remote from the idioms
of Western civilization, that must remain behind the horizon of our
understanding, unless the system of 12 equal semitones in the octave is
disposed of, and a better approximation is substituted for it.
The word octave, which denotes the fundamental distance (and similarity)
between the notes sung by men and women simultaneously when they join in a
common hymn or song, testifies to a specified musical tradition with scales in
which the eighth note is identified with the first. The Greeks did not pin down
music in one scale of seven (8 - 1 = 7). They called this
relation diapason, that is "through all", and by so doing they put into
evidence the idea that the whole variety of notes is contained in a sequence
between the first and the last note of a disapason. Nowadays the two notes
separated by this interval are known to have frequencies in the relationship of
1:2, the higher note having double the frequency of the lower. Such notes, in
spite of their differences, are identified as having the same musical value,
nowadays as well as among the ancient Greeks.
In what follows I take for granted that the reader is acquainted with the names
of the notes, A, C, D, E, F, G, A (or la, ti, do, re, mi, fa, so, la) and their
lowering and raising by signs called flats ( ) and sharps ( ) and sharps ( ): A-flat = A ): A-flat = A ,
C-sharp = C ,
C-sharp = C , and so forth. Where necessary I have added refinement. , and so forth. Where necessary I have added refinement.
Pythagoras is reported to have systematized the collection of notes by selecting
a certain specified interval relationship and ordering a sequence of notes
according to this relationship, with the rejection or exclusion of all notes not
entering this order. The selected relationship was the one that is presently
called the perfect fifth, the notes in question having frequencies in the
proportion 2:3. Thus the number 3 comes in (in spite of the historical name
fifth). The series of notes arranged by this interval relationship was
F : C : G : D : A : E : B
The sequence may be continued to the right, where sharps come in:
E : B : F : C : C : G : G ..., ...,
or to the left, where flats come in:
...D : A : A : E : E : B : B : F : C. : F : C.
Obviously this was a one-dimensional series. The only true consonances to be
found were in the octaves, in the perfect fifths and, in a lesser degree, in the
fourths. The relationship C:E (in numbers 64:81) was considered to be a
discord, and so it was in Pythagoras' linear system.
In the Renaissance period singers and composers of polyphonic music discovered
that by a slight alteration of Pythagoras' E one arrived at a perfect consonance
of C and E. This was the concord of notes with frequencies in the relationship
4:5 (64:80), where the number 5 comes in (the whim of history makes us call the
interval 4:5 a perfect third!) Accordingly one is led to a two-dimensional
specification of the legitimate notes with concordant relationships, as follows:

In this field one meets two kinds of semitones, major semitones - such as C :
D and D : E :
D and D : E - and minor semitones - such as D : D - and minor semitones - such as D : D , and E , and E : E. In the major
semitones the frequency ratio is 15:16; in the minor semitones the ratio is 24:25.
Obviously this procedure leads to an innumerable crowd of notes; and, although
in the human voice there is no restriction whatever, on an instrument it is not
possible to provide separate strings, pipes, or keys for all of them. There is
the slight difference of notes on different lines bearing the same name. In an
early age musicians agreed to discard this difference. In the 16th century
Gioseffo Zarlino said that one should adjust the sequence of "fifths" in C : G :
D : A : E in order to have a perfect concord between C and E. This was a very
slight readjustment, perceptive to a very acute ear but not a disturbing
nuisance. : E. In the major
semitones the frequency ratio is 15:16; in the minor semitones the ratio is 24:25.
Obviously this procedure leads to an innumerable crowd of notes; and, although
in the human voice there is no restriction whatever, on an instrument it is not
possible to provide separate strings, pipes, or keys for all of them. There is
the slight difference of notes on different lines bearing the same name. In an
early age musicians agreed to discard this difference. In the 16th century
Gioseffo Zarlino said that one should adjust the sequence of "fifths" in C : G :
D : A : E in order to have a perfect concord between C and E. This was a very
slight readjustment, perceptive to a very acute ear but not a disturbing
nuisance.
Rather bigger are the differences between notes such as D and C and C or G
or G and A and A ,
which are separated by three intervals in a vertical column. If one can afford
only a string or a pipe for G ,
which are separated by three intervals in a vertical column. If one can afford
only a string or a pipe for G , and not one for A , and not one for A , one can sound the perfect
common chord E : G , one can sound the perfect
common chord E : G : B but not the chord A : B but not the chord A : C : E : C : E . The increasing demand
that the chords be available in all keys led to a compromise. The present equal
temperament is based on the decision to disregard these differences, thus
identifying all notes bearing the same names and every fourth in the vertical
columns. Thus one is left with a collection of 12 notes. (Notes that duplicate
notes already put down in order places are in parentheses.) . The increasing demand
that the chords be available in all keys led to a compromise. The present equal
temperament is based on the decision to disregard these differences, thus
identifying all notes bearing the same names and every fourth in the vertical
columns. Thus one is left with a collection of 12 notes. (Notes that duplicate
notes already put down in order places are in parentheses.)

All semitones are leveled, and the ratio is very approximately 17:18. This
equal temperament was advocated by Vicenzio Galileo, in the 16th century. The
exact figures to four decimal places were calculated by Simon Stevin early in
the 17th century. Not before the middle of the 19th century was the equal
temperament universally accepted.
No doubt this equal temperament with its perfect cyclic symmetry has rendered
great services in the evolution of Western musical civilization. One must
recognize this. On the other hand, many musicians are aware of the deficiency
of the chords sound on the pianoforte and the organ that have been tuned
according to the duodecimal temperament. Their complaint is the same as the
objection of the 17th- and 18th-century musicians who refused to have their
beautiful harmonic consonances spoiled by such a compromise. One of them was Christiaan Huygens, who lived in the 17th
century. He was a very fine musician, but he also happened to be a mathematical
genius. As a mathematician he discovered a new harmonic cycle (nouveau cycle
harmonique) when, in attempting to preserve the difference between major
and minor semitones, he took just this difference as an elementary unit for the
even division of the octave. This same unit is the excess of an octave over
three perfect thirds. It is about half the minor semitone and one-third of the
major semitone. Thus it is one-fifth of a whole tones, and Huygens called it
diesis. It follows that the octave is partitioned into 31 elementary steps.
The choice of 31 notes to represent the boundless meshwork of notes related by
the ratio numbers 2, 3, and 5 evidently means the adoption of another
identification of notes instead of the identification of flats and sharps found
in the black keys of the ordinary keyboard (C and D and D , and so forth). Indeed, in
Huygens' new cycle notes such as B-double-sharp and D-double-flat are taken to
be identical. Other examples are found in A , and so forth). Indeed, in
Huygens' new cycle notes such as B-double-sharp and D-double-flat are taken to
be identical. Other examples are found in A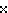 , and G , and G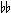 , in E , in E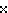 , and G , and G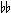 ,
D ,
D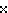 and F and F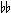 . The mesh in the net occupied by the 31 notes is as follows: . The mesh in the net occupied by the 31 notes is as follows:

One finds the seven basic notes A, B, C, D, E, F, G, their flats and sharps,
their double flats and double sharps, ruling out two double flats that are
identical to two double sharps, and vice versa.
Such a multitude of notes was far too much for the comprehensive faculties of
Huygens' contemporaries, and his discovery was left to oblivion. Yet, he made
another very significant observation. He remarked that, besides a faithful
rendering of the perfect third, his harmonic cycle also provided a nearly exact
reproduction of the perfect seventh. The perfect seventh is the interval of the
fourth and the seventh harmonic notes of a string. It is a concord in which the
number 7 comes in. Huygens claimed that it was just as valid and legitimate as
the other perfect intervals used in music and a beautiful concord, but
contemporary public opinion was against him. This repudiation of the perfect
seventh was not unlike the disqualification of the perfect third as a concord by
medieval people.
In the field of notes related by the numbers 2, 3, and 5, one finds pairs -
such as C and A-sharp - related by the numbers 128 (= 27) and 225 (= 32 ×
52). Owing to the complexity of the latter number, the interval might be taken
to sound a discord. But next to 225 lies 224 (25×7), and 128:224 = 4:7. This
simple ratio fully qualifies the interval as a concord, and Huygens' point was
that if his cycle were adopted, the number 225 would be readjusted to a very
near approach to 224. Huygens was aware of latest possibilities and beauties.
As an example he pointed out the beauty of the chord B : E : G : E : G . This is a
marvellous remark, and in his days it must been very shocking indeed, because
every 17th-century professional musician would have denounced the chord as
utterly discordant. . This is a
marvellous remark, and in his days it must been very shocking indeed, because
every 17th-century professional musician would have denounced the chord as
utterly discordant.
Nowadays there is a new demand that the system underlying our music be
improved. Well known is the attempt by Alois
Hába. He was aware that in order to preproduce native songs of his
countrymen in Czechoslovakia he needed a finer grain, so to speak, and
therefore he halved the equal semitones. He tried to use quarter-tones.
However, it is clear that by simply adding 12 more notes between the existing
12 notes one cannot improve the harmonic relationships and the musical quality
of the original 12 notes. What one needs for improvement is not quarter-tones
but fifths of tones - the system Huygens used.
Again, Bela Bartók, the Hungarian composer who died in 1945 in the United
States, recognizing the value of the Hungarian peasant music both as a living
tradition and as a source of inspiration for modern music, stated that he over
and over again met the interval of the harmonic seventh and that he therefore
laid at the bottom, as a basic foundation for music, a chord of four notes,
adding the perfect seventh to the common chord. Bartók's testimony carries great
weight, for he was one of the very greatest modern composers. Therefore, for the
evolution of music, it is very urgent that we find an equal temperament
suitable for the reproduction of Bartók's fundamental chord, which may be
specified by the harmonic numbers 4:5:6:7. The "tricesimoprimal" equal
temperament discovered by Huygens 3 centuries ago fulfills the requirement.
The aim of an equal temperament is the reproduction of certain intervals, which
are chosen because they are considered fundamental, as integer manifolds of one
single unit. This means that the problem is, given the measures of the intervals
as certain numbers, to find their common divisor. Of course, it is well known
that the musical intervals are represented by irrational numbers and that such
numbers can never have a common divisor. Thus we must try to find an approximate
divisor. The octave (1:2) measures, by definition, O = 1200 cents (the cent is
the hundredth part of an equal semitone). The perfect fifth (2:3) has Q = 702
cents. The perfect third has T = 386 cents, and the perfect seventh S = 969
cents. Any divisor common to two numbers is also a divisor of their difference.
Now, looking at
| O - 3T | = 42 | = 1 × 42
| | 2T - Q | = 70 | = 2 × 35
| | O - S | = 231 | = 6 × 38.5
| | T | = 386 | = 10 × 38.6 |
one finds that T must have 10 units; O = 31 units; Q = 18 units; and S = 25
units. The result O = 31 units, whence 1 unit = 38.7 cents, fully confirms the
discovery of Huygens. It could not have failed to do so.
The question of how to handle the harmonic seventh in music has been raised
several times. The use of it has been advocated by several authors, beginning as
early as the middle of the 18th century. Among them was Giuseppe Tartini in Padova, who allotted this
note a place in the gamut. Accidentally, it happened that in those years the
duodecimal temperament started its conquest of Western music. It could
reproduce intervals of 900 and 1000 cents, but not 969 cents, as required by
the harmonic seventh. The duodecimal temperament therefore inhibited the use of
Tartini's seventh. The tricesimoprimal temperament had never received any
attention, and therefore Tartini's attempt was doomed to fail, and it also fell
into oblivion. The time for recollection might now have come.
From the mathematical side, Leonhard Euler, a
contemporary of Tartini - neither known to the other - showed another method
for introducting the seventh into the structure of actual music. Euler was also
unaware of Huygens and his harmonic cycle of 31.
Giuseppe Tartini left us a means for notation on the stave. He introduced
half-flats and one-and-half-flats. The perfect seventh on G is slightly flatter
than the discordant F, and we may call it F-minus, or F-half-flat. The perfect
seventh on C is slightly flatter than B-flat, and we may call it B-flat-minus or
B-one-and-a-half-flat. Tartini's sign for a half-flat is a hook pointing down,
and his one-and-a-half-flat is a certain contraction of this hook with an
ordinary flat (Fig. 1).

In the tricesimoprimal temperament, F-half-flat is identified with E-sharp.
Musicians have a certain liking for connection a relation of a sixth with the
letters G and E. Therefore it might be safer to write F-minus instead of
E-sharp. The same remark applies to the use of B-flat-minus rather than A-sharp
if one meets the harmonic seventh related to C.
Obviously one could benefit by having a notation for a half-sharp too. The
perfect seventh below C is a trifle sharper than D. Let us call it D-plus, or
D-half-sharp. Again, the perfect seventh below B is a trifle sharper than
C-sharp, call it C-sharp-plus, or C-one-and-a-half sharp. The sign for a sharp
having two vertical strokes, it might be natural to write one-half sharp with a
single vertical stroke, and similarly, one-and-a-half sharp with three vertical
strokes. The subharmonic primary chords with four notes would therefore show on
the stave as they do in Fig. 2.

A sequence of notes proceeding by fifths of a tone is shown below in Fig. 3
twice, first the available signs of Tartini, second with available sharps. At
once the identity, in the tricesimoprimal temperament, of, for example, E-flat
and D-sharp-plus or E-double-flat and D-one-half-sharp, is obvious.

I return to the two-dimensional representation of all the notes related by the
numbers 2, 3, and 5. If we now recognize the harmonic seventh as a legitimate
concord, there is evidently good reason to extend the representation to a
three-dimensional one. That will appear as a kind of three-dimensional
chessboard. Crystallographers would speak of a crystal lattice with notes
instead of atoms. In crystals we meet a certain periodicity of structure and
elementary cells are reproduced over and over again, so that not all atoms are
different, and the variety is a finite variety only. In a similar way, by
establishing identities between various notes, the threefold endless multitude
of notes in the harmonic lattice is reduced to a finite set (Fig. 4).

In addition to the identification of notes in the two-dimensional harmonic plane
of relationships made by threes and fives, therefore, identifications related to
7 and one or both of the others. We have already come across the identification
of 225 = 32 × 52 and 224 = 25 × 7,
that is, the identification of A-sharp and
B-flat-minus relative to C. Another identification is reasonable, that of 343 =
73 and 341 1/3 = 1024/3 = 210/3. In relation to C, these notes come out as
G-double-flat-minus and F. Three such identities, or - speaking geometrically,
three identity vectors - delimit a unit cell in the boundless three-dimensional
field.
The foregoing sections dealt with the history and the systematics of the problem
of equal temperament. Now the practical problem is before us to put the insights
into practical use. Of course one wants to be in a position to have all the
notes available ready for use at one time. For an organ there is no specific
difficulty in providing more pipes. The valves and opened and shut by
electropneumatic devices. The problem lies in the construction of the keyboard,
and in the tuning of the pipes. The keyboard is shown in Fig. 5. There are two
manuals, the second being placed behind the first, joining it at the same level,
but rising at an increasing inclination, steeper than the first. The keys are
arranged like tiles on a roof, each key midway between a lower pair and a higher
pair of keys. The keys in a horizontal row sound notes with distances of whole
tones between them. Next to E one finds D and F . In stepping from E to F one
finds the next higher horizontal row, which ontains G, A, B, C . In stepping from E to F one
finds the next higher horizontal row, which ontains G, A, B, C , D , D , E , E ... The
key for E ... The
key for E is just in front of and lower than the key for F. This shows the
situation of the steps of one diesis, that is, one-fifth of a tone. Keys for a
series of notes such as D, D-plus, D-sharp, E-flat, E-minus, and E lie in a
straight tier running away up the keyboard. is just in front of and lower than the key for F. This shows the
situation of the steps of one diesis, that is, one-fifth of a tone. Keys for a
series of notes such as D, D-plus, D-sharp, E-flat, E-minus, and E lie in a
straight tier running away up the keyboard.
The keys have been coloured to facilitate orientation. The lettered notes A, B,
C, D, E, F, G have white keys, inconformity with ordinary keyboards. The black
keys of the ordinary keyboard appear here in pairs, for example, C and D and D , D , D and E
and E , and so forth. Other notes have blue keys. It happens that every white
key lies in a straight rising tier between two blues: D between D-minus and
D-plus, E between E-minus and E-plus (= F , and so forth. Other notes have blue keys. It happens that every white
key lies in a straight rising tier between two blues: D between D-minus and
D-plus, E between E-minus and E-plus (= F ), F between F-minus (= E ), F between F-minus (= E ) and
F-plus, and so forth. In all there are 7 × 1 whites, 7 × 2 blues, and 5 × 2
blacks, or 31 keys per octave. ) and
F-plus, and so forth. In all there are 7 × 1 whites, 7 × 2 blues, and 5 × 2
blacks, or 31 keys per octave.
In order to facilitate playing, every note is represented by two keys. Therefore
there are 11 horizontal rows. The keys in the lowest row have two replicas, one
in the middle row and one in the highest row. Thereby the little finger and the
thumb may find the keys they need in one range, the three long fingers may find
their wants in a higher range. Pairs of keys in a similar relative position
always bear the same interval. Therefore is it not necessary to change the
fingering when one is playing various scales or melodies at different pitches.
For transposing one simply displaces the hand in a uniform translation.
Besides the straight horizontal rows and the straight upward tiers there are
skewed tiers. Rising to the right, one finds ascending major semitones: A-minus
(= G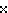 ), A ), A , B, C, D , B, C, D , E , E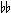 (= D-plus), D
(= D-plus), D (= E-minus), E (= E-minus), E (= F-minus), F-plus (=
G (= F-minus), F-plus (=
G ), G ), G , G natural. Thus the interval of the fifth C : G in one tier is divided
into six steps; in the other tier it is divided into nine steps. The fifth being
divided into six parts, it may also be divided into three equal parts. These are
superseconds, which have the relationship 7:8. They are elementary steps in the
gamelan of Java and Bali. Again, the
fifth may be divided into two equal parts. The result is a pair of "thirds"
intermediate between minor and major thirds. These intermediate thirds make a
very beautiful rendering of the cuckoo's call. In human civilization they are
used in music of the Arabs according to the teaching of the famous medieval
musician Zalzal. Thus the tricesimoprimal temperament provides means for a
synthesis of many musics. The pedal (Fig. 6) shows an arrangement along lines
similar to those of the manuals. , G natural. Thus the interval of the fifth C : G in one tier is divided
into six steps; in the other tier it is divided into nine steps. The fifth being
divided into six parts, it may also be divided into three equal parts. These are
superseconds, which have the relationship 7:8. They are elementary steps in the
gamelan of Java and Bali. Again, the
fifth may be divided into two equal parts. The result is a pair of "thirds"
intermediate between minor and major thirds. These intermediate thirds make a
very beautiful rendering of the cuckoo's call. In human civilization they are
used in music of the Arabs according to the teaching of the famous medieval
musician Zalzal. Thus the tricesimoprimal temperament provides means for a
synthesis of many musics. The pedal (Fig. 6) shows an arrangement along lines
similar to those of the manuals.
Fig. 5

The tuning of the pipes is made by thirds. The deviation from perfect consonance
is so small that, owing ot the acoustic coupling by the intermediate air, two
pipes - such as A and C - sounded together do not produce beats. Therefore an
electric ocillating generator is first tuned against the pipe A to a perfect
third. This is done by means of the Lissajous figure shown on the screen of an
oscillograph which puts the sound of the pipe against the oscillations of the
electric generator. If the generator is oscillating at the correct frequency,
the pipe C - sounded together do not produce beats. Therefore an
electric ocillating generator is first tuned against the pipe A to a perfect
third. This is done by means of the Lissajous figure shown on the screen of an
oscillograph which puts the sound of the pipe against the oscillations of the
electric generator. If the generator is oscillating at the correct frequency,
the pipe C is sounded and its sound taken to the oscillograph. The pipe is
adjusted until the resulting Lissajous figure shows the required number of
beats, which might be any number, for example, one in seven seconds, or one in
five seconds, as the case may be. is sounded and its sound taken to the oscillograph. The pipe is
adjusted until the resulting Lissajous figure shows the required number of
beats, which might be any number, for example, one in seven seconds, or one in
five seconds, as the case may be.
The 31-keyed organ has now been
installed in Teylers Museum at Haarlem. It was built by B. Pels en Zoon,
Alkmaar, Netherlands. It has a second console with ordinary keyboards. By
electrical switchings, these keyboards can be connected to special selections
of the complete scale. One of these selections is the one shown previously,
with E and G and G . It provides the notes as used and
conceived by the 17th and 18th century composers and it thereby restores the
ancient beauty of their creations. This is the console looking back to the
classical past. . It provides the notes as used and
conceived by the 17th and 18th century composers and it thereby restores the
ancient beauty of their creations. This is the console looking back to the
classical past.
Recitals of ancient classical music are regularly presented to the public. In
addition, the works of modern composers who avail themselves of the new
possibilities (Jan van Dijk,
Henk Badings, Paul Ch. van Westering,
Martinus J. Lürsen, and
Arie de Klein) have been executed at the
console with the new keyboards. That is the console looking to the future.

Adriaan Daniël Fokker, October 1955
|
















 ) and sharps (
) and sharps ( ): A-flat = A
): A-flat = A , and G
, and G , in E
, in E
