Francisco de Salinas (1513-1590)
Salinas was organist, theoreticus en professor in de muziek aan de universiteit
van Salamanca. Hij werd geboren op 1 maart 1513 in Burgos en was blind sinds
ongeveer zijn tiende jaar. Hij verbleef lange tijd in ItaliŽ waar hij abt van
het klooster St. Pancras de Rocca Salegno in het Koninkrijk Napels werd.
Salinas en Gioseffo Zarlino worden
beschouwd als de eersten die de middentoonstemming in wiskundig precieze termen hebben
beschreven. In zijn grote werk De musica libri septem (1577), geschreven
in het Latijn, beschrijft hij drie soorten middentoonstemmingen die hij
geschikt acht voor toetsinstrumenten, te weten de 1/3-, 1/4- en 2/7-komma
middentoonstemming. De eerstgenoemde, waarin elke kwint 1/3 komma ofwel 7 cent
kleiner is dan de zuivere kwint, heeft unieke eigenschappen ten opzichte van de
andere middentoonstemmingen.
Het is een poging om een systeem te vinden waarin niet alleen de 'genero
cromatico' (Fis, Cis, Gis, Bes en Es), maar ook de 'genero enarmonico'
(Ges, Des, Dis, As, Ais, Ces en Eis) mogelijk is. Dit was al mogelijk op het
'archicembalo' met 31 toetsen, dat werd beschreven door Zarlino in diens
Istitutioni harmoniche, maar Salinas vond een 19-toons toetsenbord
praktisch beter uitvoerbaar.
In dit systeem is het verschil tussen een kruis en zijn enharmonische mol
extreem: in feite wordt elke toon in drie gelijke stappen verdeeld, waarvan de
eerste stap de chromatische en de tweede de diatonische kleine
secunde vormt. Bijvoorbeeld vanaf de C: de eerste stap is Cis, de tweede is de
Des. Als gevolg van de 1/3 komma verkleining klinken de kwinten nog onzuiverder
dan in de gewone middentoonstemming en dat was ook de bedenking van Salinas,
hij vond ze minder sonoor en 'kwijnender' klinken, maar nog niet 'beledigend
voor het gehoor'. De reine kleine tertsen in die
temperatuur maken hem echter wel gemakkelijk te stemmen. De tonen zijn vrijwel
gelijk aan die in de verdeling van het octaaf in 19 gelijke delen (1/3 tonen).
Dus door 19 toetsen te gebruiken voorkom je de wolfskwint van de gewone
middentoonstemming. De stemming van Salinas werd bestudeerd en gewaardeerd
door ondermeer de Nederlander Quirinus van Blankenburg (18e eeuw), Helmholtz (19e eeuw)
en veel microtonale componisten uit de 20ste eeuw.

Foto: standbeeld van Salinas in Salamanca.
Hij verklaart in zijn boek de komma-verdeling van de drie stemmingen, die hij
het meest bruikbaar acht. Het syntonisch komma van 21.506 cents, ofwel het
verschil tussen de kleine grote secunde (10/9) en de grote grote secunde (9/8)
wordt bij de eerste stemming in 3 delen verdeeld waarna 1 deel bij de
kleine opgeteld en 2 van de grote afgetrokken wordt. Bij de tweede wordt het
komma in 7 delen gesplitst, waarvan 3 bij de kleine opgeteld en 4 bij de grote
in mindering gebracht wordt. Tenslotte de laatste, de 1/4-komma, of "gewone"
middentoonstemming, heeft het komma in twee gelijke delen verdeeld, waardoor de
twee grote secundes even groot worden, vandaar de naam middentoon.
| 1/3-komma middentoon
| 2/7-komma middentoon
| 1/4-komma middentoon
| | C | 0.000 | (1/1) | 0.000 | (1/1) | 0.000 | (1/1)
| | C# | 63.504 | | 70.672 | (25/24) | 76.049
| | D | 189.572 | | 191.621 | | 193.157
| | Eb | 315.641 | (6/5) | 312.569 | | 310.265
| | E | 379.145 | | 383.241 | | 386.314 | (5/4)
| | F | 505.214 | | 504.190 | | 503.422
| | F# | 568.717 | (25/18) | 574.862 | | 579.471
| | G | 694.786 | | 695.810 | | 696.578
| | G# | 758.290 | | 766.483 | | 772.627 | (25/16)
| | A | 884.359 | (5/3) | 887.431 | | 889.735
| | Bb | 1010.428 | | 1008.379 | | 1006.843
| | B | 1073.931 | | 1079.051 | | 1082.892
| | C | 1200.000 | (2/1) | 1200.000 | (2/1) | 1200.000 | (2/1)
|
A.J. Ellis vermoedt dat Salinas met zijn beschrijving van de 1/3-komma
temperatuur een vergissing maakte en ondanks de ondubbelzinnige bewering van
het vergroten van de kleine grote secunde met 1/3 komma en het verkleinen van
de grote met 2/3 komma, dat hij eigenlijk het omgekeerde moest bedoelen. Hij
kon immers omdat hij blind was, een fout in een figuur niet
zien. Zijn bedoeling zou zijn geweest om de tritonus gelijk te maken aan drie
hele tonen. Dan komen we uit op de 1/6-komma middentoonstemming waarin de
tritonus 590.224 cents (45/32) is, en de hele toon 196.741 cents. In de
1/3-komma middentoonstemming bestaat de tritonus uit twee grote hele tonen plus
een kleine, wat eigenlijk een overmatige kwart is, met 568.717 cents (25/18).
Salinas noemt deze verhouding inderdaad, en heeft daarmee de tritonus
gelijkgesteld aan de helft van een octaaf na vermindering met een grote
diŽsis (648/625), wat volgens Ellis niet klopt. De 1/6-komma
middentoonstemming komt al erg dicht bij de evenredig zwevende temperatuur.
Salinas was ook een groot kenner en bewonderaar van de Griekse toongeslachten,
waarover hij in zijn boek uitweidt, en waarvan het enharmonische zijn favoriet
was. Zijn enharmonische tetrachord luidt
1/1 25/24 16/15 4/3; intervallen:
25/24 128/125 5/4. Zijn stemming met 24 tonen per octaaf genaamd
"instrumentum perfectum" omvat het enharmonische, chromatische en diatonische
toongeslacht:
1/1 25/24 16/15 10/9 9/8 75/64 6/5 5/4 125/96 4/3 25/18 45/32 64/45 36/25 3/2
25/16 8/5 5/3 125/72 225/128 16/9 9/5 15/8 125/64 2/1.
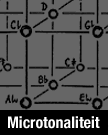
Het tonenrooster is als komma's buiten beschouwing gelaten worden en de E naar C
getransponeerd wordt (kwinten horizontaal, grote tertsen verticaal):
F# C# G#
D A E B F#
Bb F C G D
Gb Db Ab Eb Bb
Ebb Bbb Fb Cb Gb
Ebb
Zie de afbeelding van deze stemming.
Hij bracht zijn enharmonische toonschaal tot leven op zijn speciale instrument
in Salamanca met 19 toetsen per octaaf (5 toetsen minder: het "instrumentum
imperfectum"). Zijn belangstelling voor antieke muziek had hij gemeen met
Vicentino, over wie hij ook schrijft in zijn boek. In Vicentino's systeem met
31 tonen per octaaf zag hij -om genoemde praktische redenen- niet veel. Salinas
stierf op 13 januari 1590 in Salamanca.
Literatuur
- Salinas, Francisco de. De musica libri septem. Mathias Gastius,
Salamanca, 1577, 1592. Reprint M.S. Kastner (ed.), Documenta Musicologica I no.
13, Bšrenreiter, Kassel, 1958.
Boeken I-IV gaan over intervallen, toonschalen en modi; boeken V-VII over
metrum en ritme.
Tekst beschikbaar in de Thesaurus Musicarum
Latinarum:
- Helmholtz, Hermann L.F. von. On the Sensations of Tone as a Psychological basis
for the Theory of Music. 2nd English edition translated by Alexander John Ellis,
based on the 4th German edition of 1877 with extensive notes, foreword and afterword:
1885. Reprint by Dover Publications, 1954.
-
"Salinas", in New Grove Dictionary of Music and Musicians, MacMillan, London, 1980.
-
Fray Luis de Leůn's beroemde
gedicht Oda a Salinas, geschreven nadat Salinas in 1573 voor hem
had getuigd voor de Inquisitie.
|